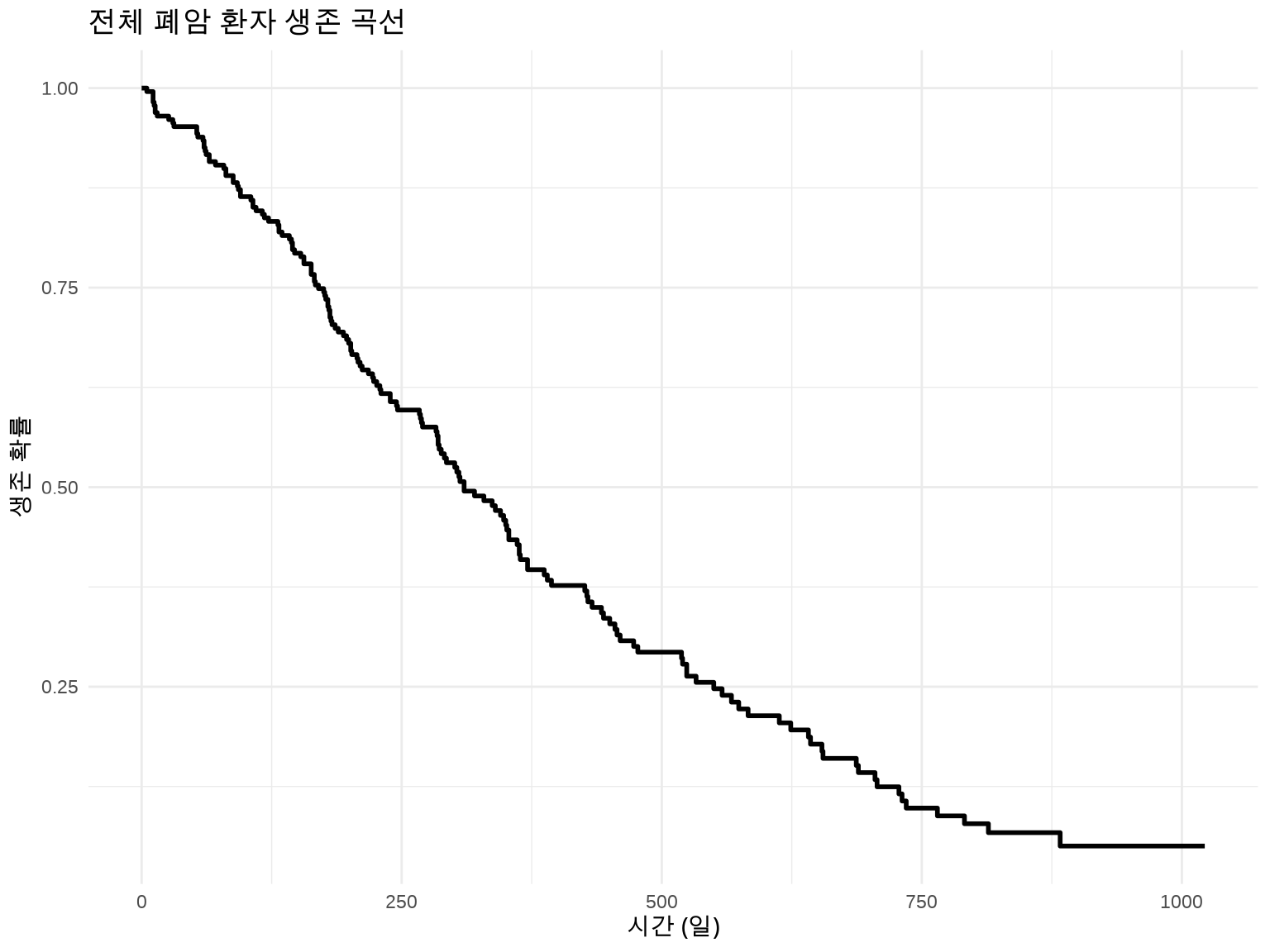
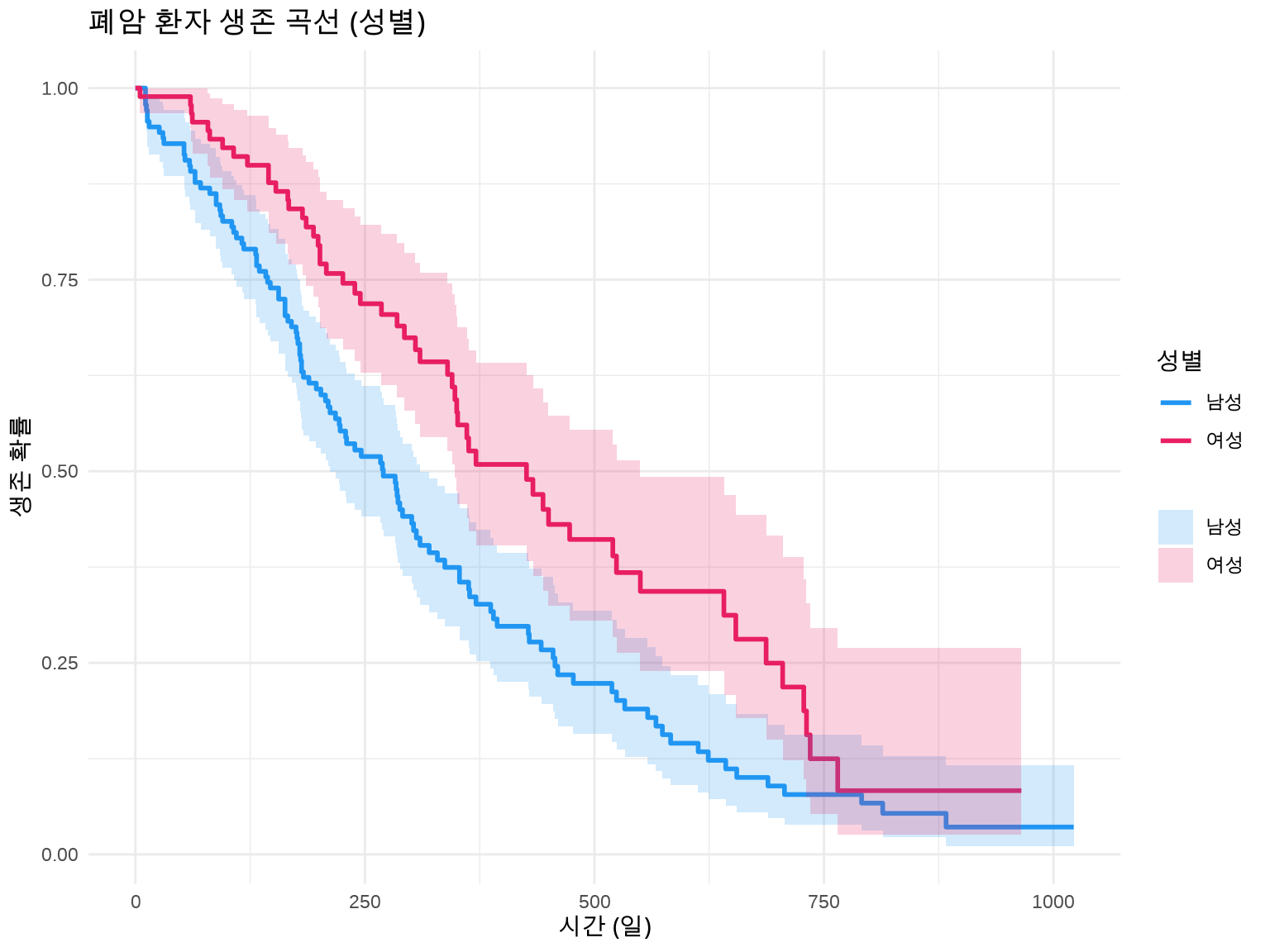
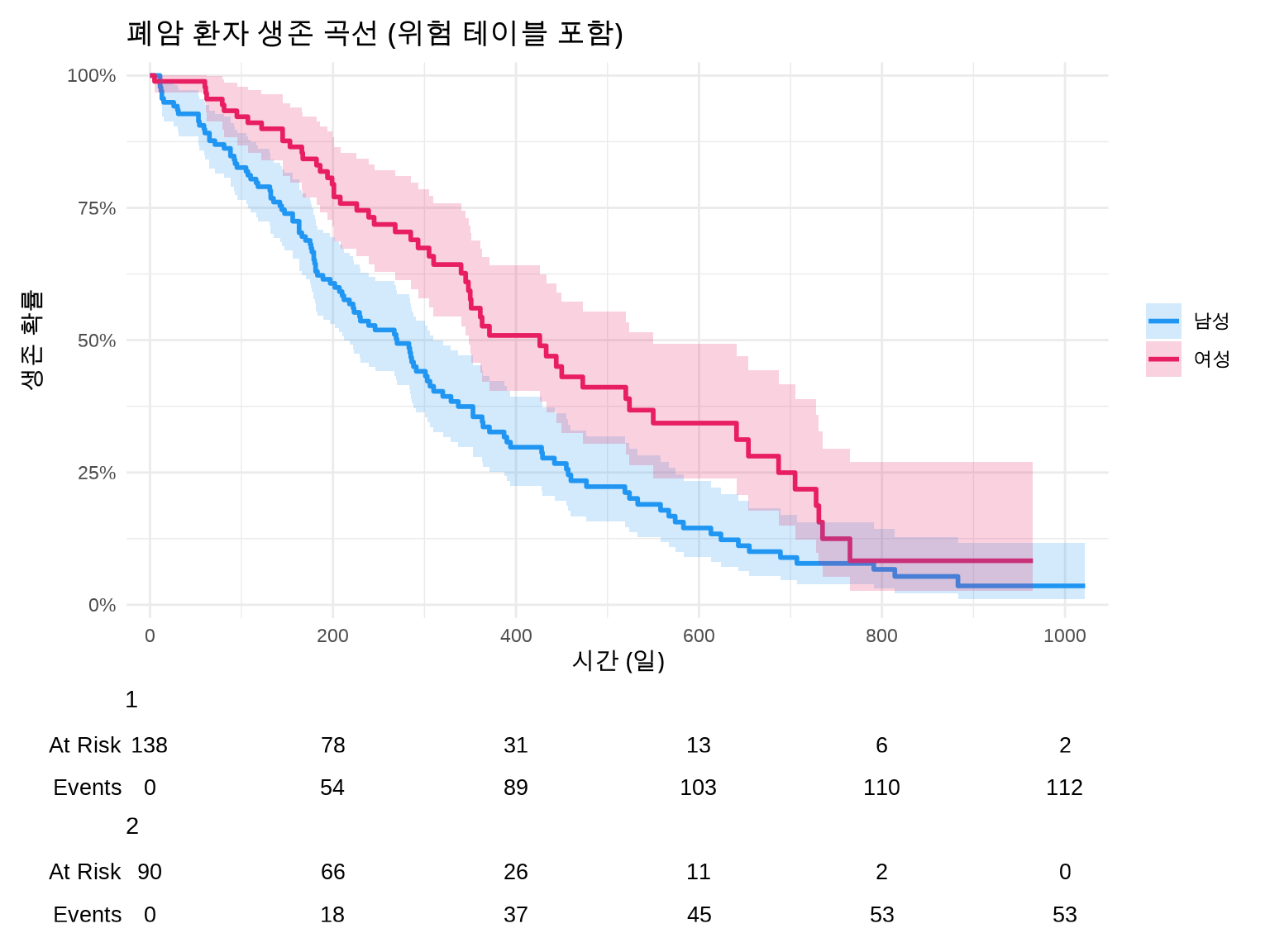
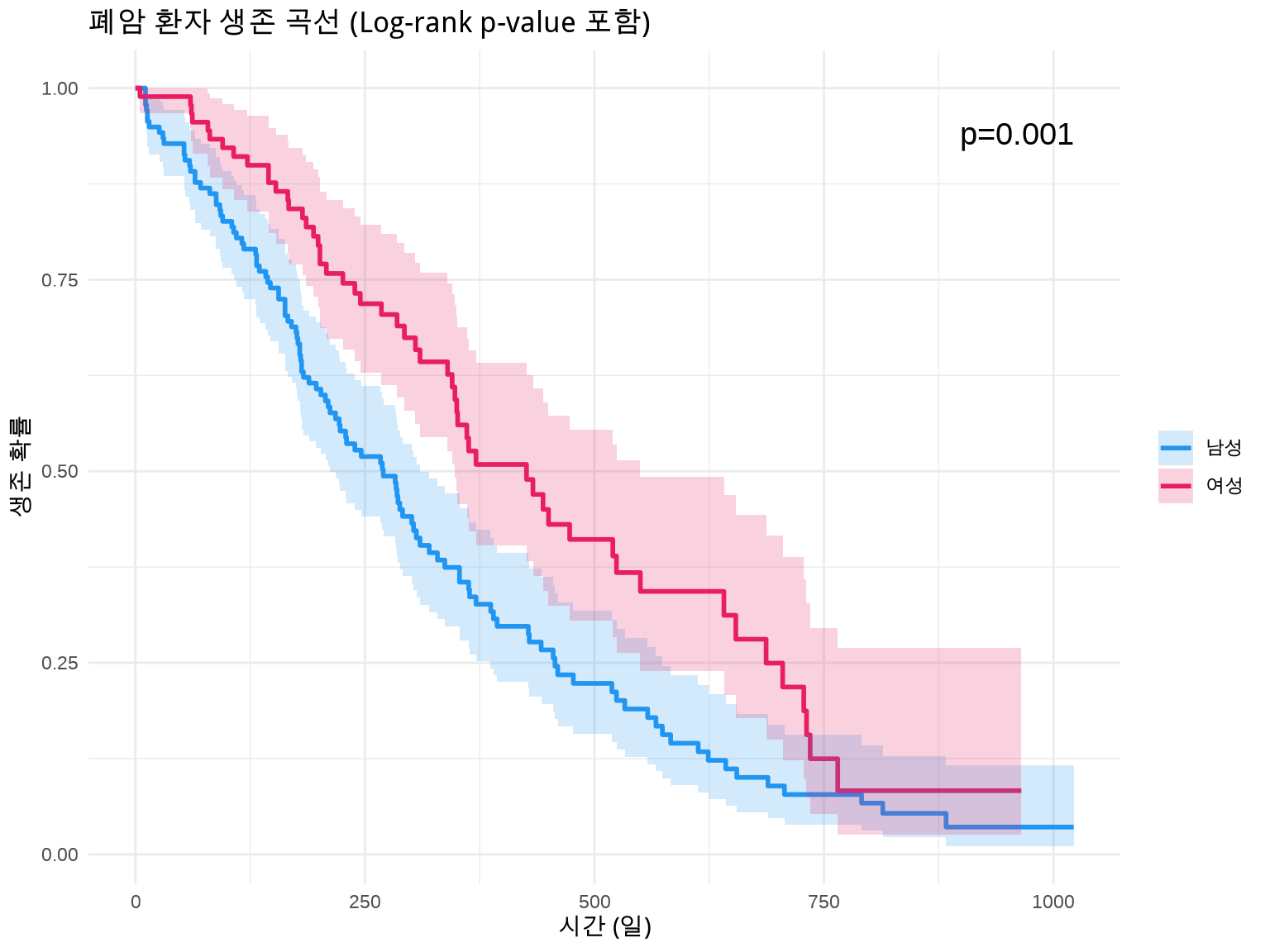
--- title: "임상 통계 시각화" author: "연세대 산업보건 연구소" date: today --- ```{r setup, include=FALSE} # 한글 폰트 설정 library(showtext) library(sysfonts) font_add_google("Noto Sans KR", "noto") showtext_auto() library(ggplot2) theme_set(theme_grey(base_family = "noto")) showtext_opts(dpi = 96) knitr::opts_chunk$set( fig.showtext = TRUE, dev = "png", dpi = 96 ) ``` # 임상 통계 및 분석 역학 시각화 ## 🎯 학습 목표 - Kaplan-Meier 생존 곡선을 `ggsurvfit` 패키지로 제작- Log-rank 검정으로 생존 곡선 비교- 메타분석 결과를 Forest Plot으로 시각화 (`metafor` )- ROC 곡선으로 진단 검사 성능 평가- Funnel Plot으로 출판 편향 탐지- 신뢰구간과 표준오차의 차이 이해## 📚 이 챕터의 실습 데이터 ### R 내장 데이터셋 불러오기 ```r library (tidyverse)library (survival) # ⚠️ 먼저 패키지 로드! library (ggsurvfit)library (metafor)# 생존 분석: survival 패키지 내장 데이터 data (lung) # 폐암 환자 생존 데이터 (N=228) data (colon) # 대장암 생존 데이터 # 메타분석: metafor 패키지 내장 데이터 data (dat.bcg) # BCG 백신 효과 메타분석 (13개 연구) # 임상시험 데이터 (시뮬레이션) <- read_csv (here ("data" , "processed" , "clinical_trial.csv" ))``` ### lung 데이터셋 상세 정보 `time` | 생존 시간 (일) | numeric |`status` | 생존 상태 (1=사망, 2=생존) | numeric |`age` | 나이 (세) | numeric |`sex` | 성별 (1=남성, 2=여성) | numeric |`ph.ecog` | ECOG 수행 점수 (0-3) | numeric |`ph.karno` | Karnofsky 점수 (의사 평가) | numeric |`pat.karno` | Karnofsky 점수 (환자 평가) | numeric |`meal.cal` | 식사 칼로리 | numeric |`wt.loss` | 최근 6개월 체중 감소 (파운드) | numeric |`?lung` 명령어로 자세한 설명을 볼 수 있습니다.## 5.1 생존 분석 (Survival Analysis) ### 5.1.1 생존 분석이란? - **Event (사건)**: 관심 있는 결과 (사망, 재발, 회복 등)- **Time (시간)**: 추적 시작부터 사건 발생까지의 기간- **Censoring (중도절단)**: 추적 종료 시점까지 사건이 발생하지 않음 - 오른쪽 중도절단 (Right censoring): 추적 중 탈락, 연구 종료 - 왼쪽 중도절단 (Left censoring): 사건 발생 시점을 정확히 모름``` 환자 A: 진단 → 5년 추적 → 사망 (event=1, time=5) 환자 B: 진단 → 3년 추적 → 탈락 (event=0, time=3, censored) 환자 C: 진단 → 10년 추적 → 생존 (event=0, time=10, censored) ``` ## 💡 왜 일반 회귀분석이 안 되나요? - 환자 B는 3년 후 탈락했지만, 실제로는 5년째 사망했을 수 있음- 이를 무시하고 "3년 생존"으로 분석하면 과소추정- 생존 분석은 중도절단을 **정보(information)**로 활용- "최소한 3년은 생존했다"는 정보를 반영### 5.1.2 Kaplan-Meier 생존 곡선 ``` S(t) = Π [1 - (사건 발생 수 / 위험 인구)] ``` ```{r} #| eval: true #| echo: true #| label: fig-km-basic #| fig-cap: "Kaplan-Meier 생존 곡선 (폐암 데이터)" # ⚠️ 중요: survival 패키지를 먼저 로드해야 lung 데이터 사용 가능! library (survival) # 1단계: 패키지 로드 library (ggsurvfit)# 2단계: lung 데이터 불러오기 data (lung) # survival 패키지의 내장 데이터 # 데이터 구조 확인 head (lung, 3 )``` ## 💡 lung 데이터 주요 변수 - **time**: 생존 시간 (일 단위)- **status**: 1 = 중도절단(censored), 2 = 사망(event) - ⚠️ 주의: 일반적인 코딩(0/1)과 반대!- **sex**: 1 = 남성, 2 = 여성- **age**: 나이 (세)- **ph.ecog**: ECOG 수행 상태 점수 (0 = 정상, 5 = 사망)- 환자 1: time=306일, status=2 → 306일 후 사망- 환자 2: time=455일, status=1 → 455일까지 추적 후 중도절단 (생존)`library(survival)` 후에는 `data(lung)` 없이 바로 `lung` 을 사용해도 됩니다!```r library (survival)head (lung) # ✅ data(lung) 없이도 작동! ``` ```{r} #| eval: true #| echo: true # 생존 객체 생성 # Surv(time, status): time=생존 시간(일), status=1(사망), 0(censored) <- Surv (lung$ time, lung$ status)# 전체 환자의 생존 곡선 <- survfit (surv_obj ~ 1 , data = lung)# 기본 생존 곡선 ggsurvfit (fit_all, linewidth = 1 ) + labs (title = "전체 폐암 환자 생존 곡선" ,x = "시간 (일)" ,y = "생존 확률" ) + theme_minimal ()``` ### 5.1.3 그룹 간 생존 곡선 비교 ```{r} #| eval: true #| echo: true #| label: fig-km-by-sex #| fig-cap: "성별에 따른 생존 곡선 비교" # 성별(sex)로 구분: 1=남성, 2=여성 <- survfit2 (Surv (time, status) ~ sex, data = lung)# ggsurvfit로 시각화 ggsurvfit (fit_sex, linewidth = 1 ) + add_confidence_interval (alpha = 0.2 ) + # 95% CI 추가 labs (title = "폐암 환자 생존 곡선 (성별)" ,x = "시간 (일)" ,y = "생존 확률" ,color = "성별" ) + scale_color_manual (values = c ("1" = "#2196F3" , "2" = "#E91E63" ),labels = c ("1" = "남성" , "2" = "여성" )) + scale_fill_manual (values = c ("1" = "#2196F3" , "2" = "#E91E63" ),labels = c ("1" = "남성" , "2" = "여성" )) + theme_minimal ()``` ### 5.1.4 위험 테이블 (Risk Table) 추가 ```{r} #| eval: true #| echo: true #| label: fig-km-risk-table #| fig-cap: "생존 곡선 + 위험 테이블" ggsurvfit (fit_sex, linewidth = 1 ) + add_confidence_interval (alpha = 0.2 ) + add_risktable (risktable_stats = c ("n.risk" , "cum.event" ), # 위험 인구, 누적 사건 size = 3.5 + labs (title = "폐암 환자 생존 곡선 (위험 테이블 포함)" ,x = "시간 (일)" ,y = "생존 확률" ) + scale_color_manual (values = c ("1" = "#2196F3" , "2" = "#E91E63" ),labels = c ("1" = "남성" , "2" = "여성" )) + scale_fill_manual (values = c ("1" = "#2196F3" , "2" = "#E91E63" ),labels = c ("1" = "남성" , "2" = "여성" )) + scale_ggsurvfit () + # 축 스케일 조정 theme_minimal ()``` ### 5.1.5 Log-rank 검정 - H0: 두 그룹의 생존 곡선이 동일하다- H1: 두 그룹의 생존 곡선이 다르다```{r} #| eval: true #| echo: true # Log-rank 검정 survdiff (Surv (time, status) ~ sex, data = lung)``` - **p-value < 0.05**: 두 그룹의 생존에 유의한 차이가 있음- **p-value ≥ 0.05**: 두 그룹 간 차이가 없음```{r} #| eval: true #| echo: true #| label: fig-km-pvalue #| fig-cap: "Log-rank 검정 p-value 표시" # p-value를 그래프에 추가 ggsurvfit (fit_sex, linewidth = 1 ) + add_confidence_interval (alpha = 0.2 ) + add_pvalue (location = "annotation" , size = 5 ) + # p-value 추가 labs (title = "폐암 환자 생존 곡선 (Log-rank p-value 포함)" ,x = "시간 (일)" ,y = "생존 확률" ) + scale_color_manual (values = c ("1" = "#2196F3" , "2" = "#E91E63" ),labels = c ("1" = "남성" , "2" = "여성" )) + scale_fill_manual (values = c ("1" = "#2196F3" , "2" = "#E91E63" ),labels = c ("1" = "남성" , "2" = "여성" )) + theme_minimal ()``` ### 5.1.6 중앙 생존 기간 (Median Survival Time) ```{r} #| eval: true #| echo: true # 중앙 생존 기간 추출 summary (fit_sex)$ table``` ```{r} #| eval: true #| echo: true #| label: fig-km-median #| fig-cap: "중앙 생존 기간 표시" ggsurvfit (fit_sex, linewidth = 1 ) + add_confidence_interval (alpha = 0.2 ) + add_quantile (y_value = 0.5 , linewidth = 0.8 , linetype = "dashed" ) + # 50% 라인 labs (title = "폐암 환자 생존 곡선 (중앙 생존 기간)" ,x = "시간 (일)" ,y = "생존 확률" ) + scale_color_manual (values = c ("1" = "#2196F3" , "2" = "#E91E63" ),labels = c ("1" = "남성" , "2" = "여성" )) + scale_fill_manual (values = c ("1" = "#2196F3" , "2" = "#E91E63" ),labels = c ("1" = "남성" , "2" = "여성" )) + theme_minimal ()``` ### 5.1.7 Cox 비례위험 모델 (Cox Proportional Hazards Model) ```{r} #| eval: true #| echo: true # Cox 모델: 성별, 나이, ECOG 수행 상태 보정 <- coxph (Surv (time, status) ~ sex + age + ph.ecog, data = lung)summary (cox_model)``` - HR = 1: 위험 동일- HR > 1: 위험 증가 (나쁜 예후)- HR < 1: 위험 감소 (좋은 예후)- `sex` HR = 0.59: 여성이 남성보다 사망 위험 41% 낮음- `age` HR = 1.02: 나이 1세 증가마다 사망 위험 2% 증가## 5.2 메타분석 (Meta-Analysis) ### 5.2.1 메타분석이란? 1. **검정력 증가**: 개별 연구보다 큰 표본 크기2. **정밀도 향상**: 더 좁은 신뢰구간3. **일관성 평가**: 연구 간 이질성(heterogeneity) 탐색4. **근거 종합**: 의사결정을 위한 최선의 추정- 여러 RCT 결과 통합- 체계적 문헌고찰 (Systematic Review)- 임상 진료 가이드라인 개발- 정책 의사결정## 💡 고정 효과 vs. 랜덤 효과 모델 - 가정: 모든 연구가 동일한 참값(true effect)을 추정- 사용: 연구 간 이질성이 낮을 때- 가중치: 큰 연구에 더 많은 weight- 가정: 각 연구의 참값이 정규분포를 따름- 사용: 연구 간 이질성이 있을 때- 가중치: 작은 연구에도 더 많은 weight### 5.2.2 Forest Plot (포레스트 플롯) ```{r} #| eval: true #| echo: true #| label: fig-forest-plot #| fig-cap: "BCG 백신 효과 메타분석 Forest Plot" library (metafor)# BCG 백신 메타분석 데이터 data (dat.bcg)# 효과 크기 계산 (Risk Ratio) <- escalc (measure = "RR" ,ai = tpos, bi = tneg, # 치료군 ci = cpos, di = cneg, # 대조군 data = dat.bcg,slab = paste (author, year, sep = ", " ))# 랜덤 효과 모델 <- rma (yi, vi, data = dat)# Forest plot forest (res,atransf = exp, # log RR → RR로 변환 at = log (c (0.05 , 0.25 , 1 , 4 )),xlim = c (- 16 , 6 ),header = "Author(s) and Year" ,xlab = "Risk Ratio (95% CI)" ,mlab = "Random-Effects Model" ,refline = 1 ) # RR=1 기준선 ``` 1. **각 행**: 개별 연구 결과 - **사각형**: 효과 크기 (크기 = 가중치) - **수평선**: 95% 신뢰구간2. **다이아몬드**: 통합 효과 크기 - 중심: 통합 추정값 - 너비: 95% 신뢰구간3. **수직 점선**: 무효과 (RR=1 또는 OR=1)### 5.2.3 이질성 평가 (Heterogeneity) ```{r} #| eval: true #| echo: true # 이질성 통계량 print (res)``` ``` I² = 85% → 전체 변동의 85%가 이질성 때문 → 연구 간 차이가 큼 → 하위그룹 분석 필요 ``` ### 5.2.4 출판 편향 (Publication Bias) ```{r} #| eval: true #| echo: true #| label: fig-funnel-plot #| fig-cap: "Funnel Plot (출판 편향 탐지)" # Funnel plot funnel (res,xlab = "Log Risk Ratio" ,ylab = "Standard Error" ,main = "Funnel Plot (BCG 백신 메타분석)" )``` - **대칭**: 출판 편향 없음- **비대칭**: 출판 편향 의심 - 작은 연구가 한쪽으로 치우침 - 음성 결과 연구가 누락되었을 가능성```{r} #| eval: true #| echo: true # Egger's regression test regtest (res)``` - **p < 0.05**: 출판 편향 의심- **p ≥ 0.05**: 출판 편향 없음### 5.2.5 ggplot2로 Forest Plot 커스터마이징 ```{r} #| eval: true #| echo: true #| label: fig-ggplot-forest #| fig-cap: "ggplot2로 만든 Forest Plot" library (tidyverse)# 메타분석 결과 데이터프레임 변환 <- tibble (study = dat$ slab,estimate = exp (dat$ yi), # RR lower_ci = exp (dat$ yi - 1.96 * sqrt (dat$ vi)),upper_ci = exp (dat$ yi + 1.96 * sqrt (dat$ vi)),weight = weights (res)# 통합 추정값 추가 <- tibble (study = "Pooled (Random-Effects)" ,estimate = exp (res$ beta[1 ]),lower_ci = exp (res$ ci.lb),upper_ci = exp (res$ ci.ub),weight = 100 <- bind_rows (forest_data, pooled_estimate)# ggplot2 Forest Plot ggplot (forest_data, aes (y = reorder (study, estimate), x = estimate,xmin = lower_ci, xmax = upper_ci)) + geom_pointrange (aes (size = weight)) + geom_vline (xintercept = 1 , linetype = "dashed" , color = "red" ) + scale_x_log10 (breaks = c (0.1 , 0.25 , 0.5 , 1 , 2 , 4 )) + labs (title = "BCG 백신 효과 메타분석" ,subtitle = "Risk Ratio (95% CI)" ,x = "Risk Ratio (log scale)" ,y = "Study" ) + theme_minimal () + theme (legend.position = "none" )``` ## 5.3 ROC 곡선 (Receiver Operating Characteristic Curve) ### 5.3.1 ROC 곡선이란? ``` 민감도 (Sensitivity) = TP / (TP + FN) # 실제 양성 중 양성으로 진단 특이도 (Specificity) = TN / (TN + FP) # 실제 음성 중 음성으로 진단 ``` - x축: 1 - 특이도 (False Positive Rate)- y축: 민감도 (True Positive Rate)- 모든 임계값(threshold)에서의 성능을 시각화### 5.3.2 AUC (Area Under the Curve) ### 5.3.3 ROC 곡선 그리기 ```{r} #| eval: true #| echo: true #| label: fig-roc-curve #| fig-cap: "ROC 곡선 (진단 검사 성능 평가)" library (pROC)library (tidyverse)# 시뮬레이션 데이터 생성 set.seed (123 )<- 200 <- rbinom (n, 1 , 0.3 ) # 30% 유병률 <- ifelse (disease_status == 1 ,rnorm (n, mean = 70 , sd = 15 ), # 환자군 rnorm (n, mean = 50 , sd = 15 )) # 정상군 # ROC 객체 생성 <- roc (disease_status, test_score)# ROC 곡선 ggroc (roc_obj, linewidth = 1.5 ) + geom_abline (intercept = 1 , slope = 1 ,linetype = "dashed" , color = "gray" ) + # 무작위 추측선 annotate ("text" , x = 0.3 , y = 0.3 ,label = paste0 ("AUC = " , round (auc (roc_obj), 3 )),size = 5 , color = "darkblue" ) + labs (title = "ROC 곡선 (진단 검사 성능)" ,x = "1 - 특이도 (False Positive Rate)" ,y = "민감도 (True Positive Rate)" ) + theme_minimal ()``` ### 5.3.4 최적 임계값 찾기 ```{r} #| eval: true #| echo: true # Youden Index로 최적 임계값 찾기 <- coords (roc_obj, "best" , ret = c ("threshold" , "sensitivity" , "specificity" ),best.method = "youden" )cat ("최적 임계값:" , best_coords$ threshold, " \n " )cat ("민감도:" , round (best_coords$ sensitivity, 3 ), " \n " )cat ("특이도:" , round (best_coords$ specificity, 3 ), " \n " )``` ## 5.4 신뢰구간 vs. 표준오차 ### 5.4.1 차이점 이해하기 ## ⚠️ 흔한 실수 - **데이터 분포 표현**: SD 사용- **평균 비교**: 95% CI 사용- **평균의 정밀도**: SE 사용### 5.4.2 시각적 비교 ```{r} #| eval: true #| echo: true #| label: fig-se-vs-ci #| fig-cap: "SE vs CI vs SD 비교" library (tidyverse)# 시뮬레이션 데이터 set.seed (456 )<- tibble (group = rep (c ("A" , "B" , "C" ), each = 30 ),value = c (rnorm (30 , 70 , 15 ),rnorm (30 , 80 , 15 ),rnorm (30 , 75 , 15 ))# 요약 통계 <- treatment_data %>% group_by (group) %>% summarize (n = n (),mean = mean (value),sd = sd (value),se = sd / sqrt (n),ci_lower = mean - 1.96 * se,ci_upper = mean + 1.96 * se# 시각화 <- ggplot (summary_stats, aes (x = group, y = mean)) + geom_point (size = 3 ) + geom_errorbar (aes (ymin = mean - se, ymax = mean + se), width = 0.2 ) + labs (title = "평균 ± SE" , y = "값" ) + theme_minimal ()<- ggplot (summary_stats, aes (x = group, y = mean)) + geom_point (size = 3 ) + geom_errorbar (aes (ymin = ci_lower, ymax = ci_upper), width = 0.2 ) + labs (title = "평균 ± 95% CI" , y = "값" ) + theme_minimal ()<- ggplot (summary_stats, aes (x = group, y = mean)) + geom_point (size = 3 ) + geom_errorbar (aes (ymin = mean - sd, ymax = mean + sd), width = 0.2 ) + labs (title = "평균 ± SD" , y = "값" ) + theme_minimal ()library (patchwork)+ p2 + p3 + plot_annotation (title = "SE vs CI vs SD 비교" )``` - **SE**: 가장 좁음 (평균의 정밀도)- **95% CI**: SE의 1.96배- **SD**: 가장 넓음 (데이터 분포)## 5.5 실전 연습문제 ## ✏️ Exercise 5.1: 생존 곡선 그리기 `survival::colon` 데이터를 사용하여:1. 치료군(`rx` )별 생존 곡선 그리기2. 95% 신뢰구간 추가3. 위험 테이블 포함4. Log-rank 검정 p-value 표시`rx` 변수는 치료법 (Obs, Lev, Lev+5FU)```{r} #| eval: false #| code-fold: true #| code-summary: "💡 정답 보기" library (survival)library (ggsurvfit)data (colon)# 생존 데이터만 (event=1: 사망, etype=2: 재발 제외) <- colon %>% filter (etype == 2 ) # death <- survfit2 (Surv (time, status) ~ rx, data = colon_death)ggsurvfit (fit_rx, linewidth = 1 ) + add_confidence_interval (alpha = 0.2 ) + add_risktable () + add_pvalue (location = "annotation" ) + labs (title = "대장암 생존 곡선 (치료법별)" ,x = "시간 (일)" ,y = "생존 확률" ,color = "치료법" ) + scale_ggsurvfit () + theme_minimal ()``` ## ✏️ Exercise 5.2: Forest Plot 만들기 ```r <- tribble (~ study, ~ or, ~ lower_ci, ~ upper_ci,"Study 1" , 0.8 , 0.6 , 1.0 ,"Study 2" , 0.7 , 0.5 , 0.9 ,"Study 3" , 0.9 , 0.7 , 1.1 ,"Study 4" , 0.6 , 0.4 , 0.8 ,"Pooled" , 0.75 , 0.65 , 0.85 ``` - ggplot2 사용- OR=1 기준선 표시- 통합 추정값은 다른 색으로```{r} #| eval: false #| code-fold: true #| code-summary: "💡 정답 보기" library (tidyverse)<- tribble (~ study, ~ or, ~ lower_ci, ~ upper_ci,"Study 1" , 0.8 , 0.6 , 1.0 ,"Study 2" , 0.7 , 0.5 , 0.9 ,"Study 3" , 0.9 , 0.7 , 1.1 ,"Study 4" , 0.6 , 0.4 , 0.8 ,"Pooled" , 0.75 , 0.65 , 0.85 %>% mutate (type = if_else (study == "Pooled" , "Pooled" , "Individual" ))ggplot (meta_data, aes (y = reorder (study, or), x = or,xmin = lower_ci, xmax = upper_ci,color = type)) + geom_pointrange (size = 0.8 ) + geom_vline (xintercept = 1 , linetype = "dashed" , color = "red" ) + scale_color_manual (values = c ("Individual" = "darkblue" , "Pooled" = "red" )) + labs (title = "메타분석 Forest Plot" ,x = "Odds Ratio (95% CI)" ,y = "Study" ) + theme_minimal () + theme (legend.position = "none" )``` ## ✏️ Exercise 5.3: ROC 곡선 비교 (도전!) ```r # 시뮬레이션 데이터 set.seed (789 )<- 150 <- rbinom (n, 1 , 0.4 )<- ifelse (disease == 1 , rnorm (n, 75 , 12 ), rnorm (n, 50 , 12 ))<- ifelse (disease == 1 , rnorm (n, 80 , 15 ), rnorm (n, 55 , 15 ))``` - 두 ROC 곡선을 다른 색으로- 각 AUC 값을 범례에 표시```{r} #| eval: false #| code-fold: true #| code-summary: "💡 정답 보기" library (pROC)library (tidyverse)set.seed (789 )<- 150 <- rbinom (n, 1 , 0.4 )<- ifelse (disease == 1 , rnorm (n, 75 , 12 ), rnorm (n, 50 , 12 ))<- ifelse (disease == 1 , rnorm (n, 80 , 15 ), rnorm (n, 55 , 15 ))<- roc (disease, test1)<- roc (disease, test2)# ggplot으로 두 ROC 곡선 ggroc (list (Test1 = roc1, Test2 = roc2), linewidth = 1.5 ) + geom_abline (intercept = 1 , slope = 1 , linetype = "dashed" , color = "gray" ) + labs (title = "ROC 곡선 비교" ,subtitle = paste0 ("AUC: Test1=" , round (auc (roc1), 3 ),", Test2=" , round (auc (roc2), 3 )),x = "1 - 특이도" ,y = "민감도" ,color = "검사" ) + theme_minimal ()``` ## 5.6 요약 및 다음 단계 ### 5.6.1 이 챕터에서 배운 내용 - Kaplan-Meier 생존 곡선- 위험 테이블 (Risk Table)- Log-rank 검정- 중앙 생존 기간- Cox 비례위험 모델- 고정 효과 vs. 랜덤 효과- Forest Plot 시각화- 이질성 평가 (I², τ²)- Funnel Plot (출판 편향)- ggplot2 커스터마이징- 민감도 vs. 특이도- AUC 해석- 최적 임계값- SE vs. CI vs. SD 차이- 올바른 사용법### 5.6.2 핵심 코드 템플릿 ```r <- survfit2 (Surv (time, status) ~ group, data)ggsurvfit (fit) + add_confidence_interval () + add_risktable () + add_pvalue ()``` ```r <- rma (yi, vi, data)forest (res, atransf = exp, xlab = "Odds Ratio" )``` ```r <- roc (disease, test_score)ggroc (roc_obj) + annotate ("text" , label = paste0 ("AUC = " , round (auc (roc_obj), 3 )))``` ## 📖 다음 챕터 1. **다중 그래프 조합**: patchwork 패키지2. **색상 선택**: 색맹 친화적 팔레트3. **폰트 및 해상도**: 출판 표준 (300 dpi)4. **테마 커스터마이징**: theme() 완전 정복5. **저장 및 내보내기**: ggsave() 최적 설정## 🔗 추가 학습 자료 ### 생존 분석 - **ggsurvfit**: [ 공식 문서 ](https://www.danieldsjoberg.com/ggsurvfit/) - **survival**: [ CRAN ](https://cran.r-project.org/web/packages/survival/) - **survminer**: [ 대안 패키지 ](https://rpkgs.datanovia.com/survminer/) ### 메타분석 - **metafor**: [ 공식 문서 ](https://www.metafor-project.org/) - **Cochrane Handbook**: [ 메타분석 가이드 ](https://training.cochrane.org/handbook) - **meta**: [ 대안 패키지 ](https://cran.r-project.org/web/packages/meta/) ### ROC 곡선 - **pROC**: [ 공식 문서 ](https://web.expasy.org/pROC/) - **ROCR**: [ 대안 패키지 ](https://cran.r-project.org/web/packages/ROCR/) ### 임상통계 전반 - **Clinical Trials**: [ ClinicalTrials.gov ](https://clinicaltrials.gov/) - **CONSORT**: [ RCT 보고 지침 ](http://www.consort-statement.org/)